If you are reading this post, chances are you have already encountered the almighty Bayes Theorem and are curious about its application and implications in real-life scenarios. It also goes without saying that you have, at least, a basic working knowledge of statistics and probabilities. If you all this is, however, entirely new to you, no worries you are in good company. I am not a statistics expert either, I just have a sizable dose of curiosity for how the application of theoretical principles affect people’s daily lives.
I got curious during a Deep Learning course in my study of MS Data Science program, when the Professor, lecturing on the ethical use of statistics, mentioned some cases where unethical application of statistics can have very undesirable consequences. He specifically pointed out the Simpson’s Paradox and the Sally Clark’s case as examples where statistical knowledge can be misleading or lead to very dire consequences when misapplied. I will leave you to read on the Sally Clack case as a classical example of ignoring Bayes Theorem.
For now, since I have made it my life’s mission to have a romantic affair with data (to get to the heart of data to extract insights and patterns: see https://datewthdata.com) by dating it, I have taken a keen interest in the dangers of misapplying the results of statistical analysis. Despite our best intentions, sometimes a lack of grasp of the nuances of a scientific principle can lead to very calamitous consequences during its application to real-life events. For this post, my focus is on Bayes Theorem, its application and significance in real life events and the perils of ignoring or misapplying it.
So what is Bayes Theorem?
Some of you may have come across it in text as Bayes Law or Bayes Rule, both are referring to the same thing: Bayes Theorem. The theorem is based on conditional probability which describes the probability of an event occurring given that a prior event has already occurred.
Bayes Theorem is, thus, the probability of an event based on prior knowledge of conditions that might be related to the event.
More succinctly, Bayes Theorem is this: the probability of A given B is equal to the probability of A times the probability of B given A over the probability of B, where A and B are independent events.
Mathematically, this may be expressed as:
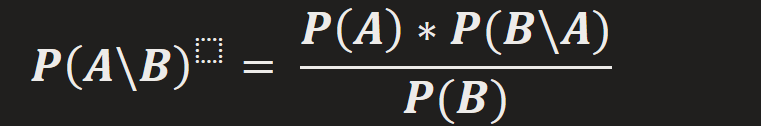
Where:
P(A\B) = Probability of event A given event B
P(B\A) = Probability of event B given event A
P(A) = Probability of event A
P(B) = Probability of event B
Key Insight: The probability of some event A, that depends on B is also very much dependent on the base probability of B and A.
The above equation gives us a means to quantitatively tell if someone is trying to pull a fast one on us by using obscure statistical terminology and jargon. In the next section I illustrate how we can use this theorem to break free from the alluring grip of statistical con men (and women: you can see I am very gender sensitive!!!).
Practical Application of Bayes Theorem
So where can we find examples to illustrate the power and significance of Bayes Theorem in everyday life? Well, the web and textbooks are replete with various areas of application of this theorem. I will, however, take just one(1) area where its effects can be very profound if misapplied or ignored, both in terms of human life and economic resources. You guess it: Healthcare!
Bayes Theorem in Healthcare: Drug administration based on alcohol test results.
For this case, let’s assume there is a certain medication that is not supposed to be administered to people who drink alcohol (test positive for alcohol). Now let’s say we are interested in finding the probability that you drink alcohol given that you tested positive for alcohol. (Note: This is a completely made up scenario to illustrate the application of Bayes Theorem)
Let’s further assume we have come up with an alcohol test that has a 99% accuracy of identifying alcohol users and 99% of accuracy of identifying people who do not take alcohol. For the purposes of this analysis, let’s assume we know that only 0.4% of the overall population drink alcohol.
99% is obviously a very high accuracy, however with only 0.4% of the population known to drink alcohol, this supposedly high-accuracy-test of detecting alcohol intake can be very misleading. But how can we truly quantify the probability that you drink alcohol given that you tested positive for alcohol using our ‘very accurate’ test kit?
Let’s turn to Bayes Theorem and do the math:
Say:
Event A = a person drinks alcohol
Event B = a person tested positive for alcohol
We need to first find the overall probability of testing positive for alcohol, that is the probability of B, P(B).
This can be worked out by adding up the probabilities of testing positive if you take alcohol and testing positive if you do not take alcohol.
Population that take alcohol = 0.4%
Population that do not take alcohol = 99.6%
Probability of testing positive if you take alcohol = 0.99 x 0.004 = 0.00396
Probability of testing positive if you not take alcohol = 0.01 x 0.996 = 0.01392
P(B) = 0.00396 + 0.01392 = 0.01788 or 1.8%
That is, based on available information and the absence of knowledge of anything else about the patient, the probability of testing positive for alcohol is 1.8%.
Now let’s apply Bayes Theorem,
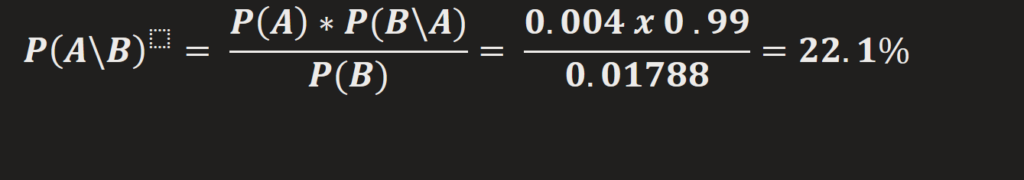
You will notice that the probability of testing positive given that you actually take alcohol is 0.3% which is the same as the overall probability of taking alcohol.
As we have shown by applying Bayes Theorem, a test that has a very high accuracy of 99% of detecting a positive case given that a patient takes alcohol, that is P(B\A) shows a very low probability of 22.1% of detecting an alcohol user given that the patient tests positive for alcohol, that is P(A\B).
So quantitively, Bayes Theorem tells us that although this alcohol test kit has a very high accuracy of 99%, in reality, 78% of the time, it will be producing false results.
Now can you imagine the number of people we could be denying essential medication if we just took the accuracy of the test kit on face value without the application of sound statistical principles, Bayes Theorem in this case? Further stretch your mind to other applications such as cancer detection, customer risk assessment for loan contracting, investment portfolio risk analysis among others and it becomes immediately apparent how important Bayes Theorem is and why ignoring or misapplying it can can prove very perilous.
As a wrap-up, always be guided by Bayes Theorem especially when you are dealing with problems that have a low overall incidence in the general population but tend to show very high probability of detecting positive cases.
That was rather a mouthful, but I hope you got something out of it! Thanks for sticking around to the end.